変形力・把握力の予測
変形量の予測について
Q.CAEとは?
A.CAEとは、Computer Aided Engineering の略で「物理現象を方程式に置き換えてコンピュータを用いて高速に解を求める」手法です。弊社では、把握力など外力によるワークの変形量を予測するために「線形静解析」のCAEを取り扱っています。このような3次元体構造の解析手法としては、一般に有限要素法(FEM)が用いられます。
Q.線形静解析とは
A.荷重の大きさが倍になると、その応答値(変位、ひずみ、応力)も倍になるようなモデルを線形であるといい、以下のような場合線形の仮定が成り立ちます。
・モデルの全ての材料がフックの法則に従っている。すなわち応力がひずみに比例している。
・変位は十分小さい、すなわちそれによる剛性変化が無視できる。
・荷重をかけている間、境界条件が変化しない、すなわち荷重は大きさも方向も分布も一定でなければならない。
Q. 有限要素法(FEM)とは?
A.有限要素法(FEM:Finite Element Method)とは数値解析手法の一つで、解析的に解くことが難しい微分方程式の近似解を数値的に得る方法です。
Q.そもそも、なぜこの取り組みを始めたのか?
A.弊社では幅広い加工範囲のワークを取り扱ってきましたが、それに伴う加工内容は千差万別です。この中でも把握力など外力による変形量を事前に予測するのは困難な領域となっていました。そこで、これらの課題を線形静解析のCAEで解決できないかと発案したのがきっかけです。一般に線形弾性の応力解析に限定すれば、有限要素法理論は既に完成していると言われおり、大きな塑性変形を伴わないチャッキング等であれば、活用できる見込みもありました。
Q.具体的な解析方法は?
A.以下の手順で解析を行います。
モデル作成→アセンブリ作成→接触条件の設定→荷重・拘束条件の設定→要素分割→解析実行
Q. 実用性は?
A. 解析では理想的なモデルや条件の設定を行います。一方、現実の現象では、解析で設定した条件のほか、取り付けガタなど様々な外的要因が絡み合っています。そのため、現実の現象を忠実に解析に反映させることに多大な時間と労力を要します。弊社では解析で得られる結果=目安と捉え、ベストではないがベターを目指すための道具として解析を活用しています。解析値と実測値との比較例については「事例を見る」をご参照ください。
Q.効果は?
A. 定性的な効果としては以下のものが挙げられます。
- 熟練者の勘や経験への依存度を減らせる
- 不具合の可能性が低くなる
- 失敗の原因追求がしやすくなる
- 現象の理解力が深まる
- 入手できない情報を保管できるようになる


三次元測定器測定結果
計測値.pdf
PDFファイル 1.6 MB
| 【結果比較】 内径真円度 0.039(解析値) 0.026(三次元測定器実測値) 外径真円度 0 (解析値) 0.009(三次元測定器実測値) 【解析条件】 ワーク仕様 材質 S45C-N(黒川除去済材) 寸法 φ528×φ440×t68 外周真円度 0 チャック仕様 方式 単動4つ爪 材質 合金鋼 概寸 W80×L220×L110 把握部 外周 把握部長さ 40mm 把握力 9000N |
●薄板ワークの把握方法・支持方法による変位分布の違い①(φ500×13t,ss400)
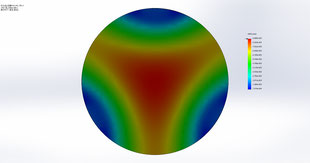

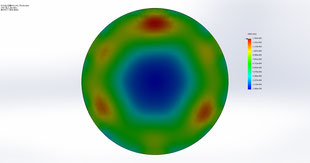
●リング状ワークの把握方法による変位分布の違い②(φ530×Φ440×50t,ss400)


把握力の予測について
Q.そもそも、なぜこの取り組みを始めたのか
A.弊社は幅広い加工範囲のワークを取り扱ってきましたが、それに伴う加工内容は千差万別です。この中でも把握力(チャック圧、把持力)の設定は勘と経験を頼りにする以外にないのが現実です。特に横型のNC旋盤で片持ち加工をする場合、その傾向は顕著で、把握力・切削条件などの設定を誤ると回転したワークが飛出し危険である上、機械・ワーク自体が損傷します。そこで、これらの課題を理論的に解決できないかと発案したのがきっかけです。
Q.具体的な計算方法は?
A. 力及びモーメントの釣り合いの式より理論上の把握力を算出し、安全率を乗じた上で実際の加工時の把握力とする独自モデルにより計算します。以下に手順を示します。
ワークの条件設定→把握条件の設定→切削条件の設定→吊り合いの式→理論把握力→安全率→必要把握力
Q. 実用性は?
A. 独自モデルに従い、弊社ではこれまで実際に加工を行ってきました。この中で安全率の設定は、実際に加工を行った上で決定され、サンプル数が多いほど、モデルの信頼性は向上します。弊社でのサンプル数は既に200を超えており、ある程度は実用的であると判断されます。詳細は「事例を見る」をご参照ください。
Q.効果は?
A. 定性的な効果としては以下のものが挙げられます。
- 熟練者の勘や経験への依存度を減らせる。
- 安全性が高くなる。
- 失敗の原因追求がしやすくなる。
- 現象の理解力が深まる。
- 入手できない情報を保管できるようになる